(new: Japanese translation available, thanks to Yuki Ozawa)
Common depth buffer setups used in 3D graphics hardware to this day are woefully inadequate for the task. One can easily get artifacts known as z-fighting even with relatively limited scene depth range. Utilization of the available depth buffer values is quite horrible: half of the resolution is essentially wasted just in the distance from the near plane to twice that (short) distance. This leads to the need to move the near plane as far as possible, which is not very desirable in itself, and it’s still not enough as soon as you need to cover just a slightly extended detail range. It’s of course completely unusable for large scale rendering, with developers having to use various tricks that bring their own bag of complications.
This article talks about the ways to set up the depth buffer so that it's able to handle blades of grass in front of your eyes while also rendering objects hundreds of kilometers in distance. It's mostly biased towards OpenGL, but most of it applies to DirectX as well.
Let’s go first into some details about the depth processing that aren’t immediately obvious, which nevertheless play a significant role in understanding the properties of depth buffering.
A common perspective depth buffer setup relies on the use of a standard projection matrix that involves setting the near and far clipping plane distances. While you can set the projection matrix in any way you want, a perspective-correct depth buffering will work only as long as the matrix satisfies certain conditions.
With the standard perspective OpenGL projection matrix, the value of w and z output from the vertex shader is usually computed as:
wp = -z
zp = z*(n+f)/(n-f) + 2fn/(n-f)
That means w ends up holding the positive depth from the camera plane, while z can be generally expressed as a linear equation:
zp = -az + b
or
zp = awp + b
Values from the vertex shader are then converted into the normalized device coordinates by dividing by w, and z thus becomes:
zndc = a + b/wp = a - b/z
After that it gets clipped to -1 .. 1 range.
DirectX uses 0..1 range for z, but the principle is the same.
Specification says that with perspective interpolation all vertex shader outputs are interpolated in perspective (by interpolating p/w and 1/w linearly and then dividing the two to get perspective-correct values), except for the value of z which will be interpolated linearly. Why is that?
It’s because the rendering API expects that you are using a projection matrix that has a 1/z term in it (the above mentioned a - b/z), and thus to interpolate it in a perspective-correct way the hardware has to (and will only) use a linear interpolation.
Now the problem is that this value is also used for the depth comparison. At the first look it may seem to be a fairly nice function to be used for depth: providing a finer resolution for the near objects, getting reduced with the distance where it’s needed less as the objects get smaller in perspective.
However, in reality the profile is horribly unsuitable because it wastes way too much of the available range for the close values. Half of the available range is packed into tiny distance from the near plane to twice the near plane distance.
If there was a possibility to turn on the perspective interpolation on the depth component (as it’s already done for other interpolants unless the noperspective qualifier is used), then we would have several good ways to radically enhance the depth buffer precision without interpolation artifacts. Alas, the hardware doesn’t seem to count with that possibility anymore, as the W-buffers has been gradually phased out.
Let’s take a look on what can be done about it using the available resources. First, what would be the ideal profile.
To avoid z-fighting artifacts, depth buffer should provide resolution that is proportional to the size of geometry needed to render a constant screen size image at different distances from the camera, across the whole depth range. Projected screen size is proportional to the reciprocal of geometry depth, 1/z. In other words, we are looking for a function whose derivative is proportional to 1/z. That function happens to be the logarithm.
To see how an ideal utilization of depth buffer values compares to the common setup, see the following graph with computed precision of the common pipeline with 32bit floats, compared to logarithmic depth buffers at 24 and 32 bits.
While the logarithmic distribution handles the 9 decades of depth detail range easily, a common depth buffer setup strides into the unusable region after its brief 4 decades. Four decades is roughly the range we can get with the normal depth buffer setup, after that the precision gets into the unusable region and the depth buffer can't resolve the depth values properly anymore. With the logarithmic buffer we have a plenty of reserve, in fact we could handle the scene with a 16 bit logarithmic depth buffer.
Note that the axes in the graph are using logarithmic scales, so anything rising faster than 10dB is actually degenerating very quickly.
Speaking of an ideal utilization, it’s desirable to add that there’s also a lower bound on the required depth buffer resolution that reflects the physiognomy of our eyes - we can’t focus on objects very close to our eyes, so there’s no need to have a micrometer resolutions for miniscule objects in front of us. This can be used to enhance the resolution elsewhere, as we’ll see later.
If the values used for depth comparison were the depth values themselves, floating point values would be good for the depth buffering technique: closer to the viewer you get values near zero, for which floating point encoding provides higher precision by keeping the number of bits in mantissa constant and adjusting the exponent. The farther you go less depth resolution you need, since the screen size of distant objects goes down by ≈1/z.
Unfortunately, the value used for depth comparison is the 1/z function itself which has the unfortunate property of eating all the resolution on breakfast and then starving till evening.
The use of floating-point values in depth buffer doesn’t bring much if used directly: there’s an increased dynamic range close to zero, but since the depth buffer already uses most of the value range in this region, it’s not useful at all.
There’s a trick that can do something about it: swapping the near and far values will make use of the increased range of floating point for the distant part, instead of the near one. This is actually very effective: the increasing resolution of floating point number close to zero neatly compensates the dwindling resolution of 1/z function.
Here’s the graph showing the resolution of reversed floating point buffer in DirectX:
Reversed 32bit floating point depth buffer brings slightly better resolution than a 24bit logarithmic buffer (a 32bit logarithmic depth buffer is roughly 20X finer), consistent across the whole 9 decades. That’s pretty great. One downside is that in comparison to a 24 bit integer buffer it consumes 8 more bits that could be otherwise used for stencil. Before, on older hardware, the use of stencil consumed twice as much memory for the framebuffer, since the next available format was padded to 32bits, with higher bandwidth required as well. However, nowadays it's not a problem - stencil is kept separate and depth buffer is optimized/packed, and the only thing that remained is a bit misleading OpenGL enum.
You will also notice I mentioned DirectX explicitly. If you try the trick on OpenGL you will see zero improvement.
As much as I am a fan of OpenGL and prefer it over DirectX, there are things in OpenGL that make me want to climb walls holding with fingernails.
Some time back someone decided that OpenGL normalized device coordinates should be in range -1 .. 1 on all 3 axes, including the z coordinate. Normally, one would place the camera into the center, projecting towards +z or -z. Z axis projects to the screen center, so it’s only logical that x and y would be symmetric, but Z?
For the screen depth axis it’s more natural to assume normalized coordinates in 0..1 range, from the camera (or the near plane) to the far plane. Especially when the depth values written into the depth buffer are also in range 0..1.
However, someone dreamed of a symmetric world and decided it should be more important to prefer the symmetry over the reason, and to have z in the -1 .. 1 range as well. Of course, then it needs to be reprojected into the depth buffer values by performing additional computation: 0.5*zc + 0.5
How this connects with the depth buffer precision issue? First, reversing the depth range does essentially nothing, because it just swaps the mapping of the near and far plane between -1 and 1, with the extra precision around the zero mapped to 2*near distance in both cases.
This can be helped by using a projection that maps the far plane to 0. Normally the 3rd row of the OpenGL projection matrix is
mapping the near plane to -1 and the far plane to 1. Changing it to
will map the far plane to 0 instead. This is essentially the reversed-depth DirectX projection matrix with an inverted sign, so that the depth function doesn't change (but it can be easily switched to 1..0 range).
Clipping still applies at 1.0, so one would have to use a custom clipping plane to clip at 0. But it can be also ignored if the situation allows it. For example, in Outerra there’s actually no need to clip geometry behind the far plane, as it’s usually set as far as possible anyway.
But using this alternative projection alone does not resolve the problem, the resolution is still miserable. The second part of the problem is the additive term in the remapping (0.5zc + 0.5). That 0.5 bias locks the floating point exponent and pretty much destroys any and all additional precision that the encoding of floating point values brings close to zero, since now there are just 24 bits of mantissa to handle the unfortunate 1/z shape. Hello, symmetry!
Fortunately, at least on Nvidia there’s a way to eliminate the bias by (indirectly) setting the mapping function via the glDepthRangedNV call with -1, 1 arguments, which effectively sets the DirectX-style mapping. Here’s the final resolution graph of a floating point depth buffer without the bias, with the far plane mapped to 0 in OpenGL. The resolution was actually measured on the 460 GTX GPU:
Unfortunately neither AMD nor Intel hardware does support the NV_depth_buffer_float extension. I was told it’s a hardware limitation, it’s not able to support arbitrary output depth values. But arbitrary isn’t needed. Since it supports DirectX depth mapping without the bias, I believe it should be entirely possible to turn off the OpenGL style remapping.
Update: glDepthRangedNV is exposed in AMD Catalyst 13.11 betav9.2 drivers
Also note that even though OpenGL 4.2+ specification removed the note saying that the core function glDepthRange arguments will be clamped to 0..1 range for floating-point depth buffers, implementations are apparently still allowed to clamp the values on use, effectively making the spec change somewhat useless. As of now the values are being clamped even on Nvidia, so we need to use glDepthRangedNV extension.
There are two issues with the above described bias-less floating point OpenGL depth buffer - the lack of universal support, and the increased memory and bandwidth requirements in case a stencil buffer is needed.
We can actually use the above mentioned ideal logarithmic distribution on all current hardware. First described on the Outerra blog - see the logarithmic depth buffer article. Thatcher Ulrich later came up with a slightly different version here.
Logarithmic depth buffer technique works by outputting the desired logarithmic value from the vertex shader, premultiplied by the value of w, to get rid of later implicit perspective division.
It’s quite easy to implement, you just need to add the following code in the vertex shader after your normal projection matrix multiply:
gl_Position.z = 2.0*log(gl_Position.w*C + 1)/log(far*C + 1) - 1;
gl_Position.z *= gl_Position.w;
or
gl_Position.z = 2.0*log(gl_Position.w/near)/log(far/near) - 1;
gl_Position.z *= gl_Position.w;
The latter is Ulrich’s variant (here referred to as “N-F”) that has a nice property of having a constant relative precision over the whole near-far range, but as we’ll see later, nice (or symmetric) isn’t always the best option.
Obviously, the constant part (2.0/log(far*C+1) or 2.0/log(far/near), respectively) can be optimized out into a constant or uniform variable.
Notice that the “C” variant doesn’t use a near plane distance, it has it set at 0.
This algorithm works well, providing excellent precision across the whole range with a huge reserve. But it also suffers on issues with long polygons close to the camera.
The problem is that the vertex shader computed value is correct only at the vertices, but the interpolated values at pixels can stray from the expected value because of two factors: non-linearity of the logarithmic function between two depth values, and the implicit linear (and not perspective) interpolation of the depth value in the rasterizer. To fix it, one has to output the correct value by writing to gl_FragDepth in the fragment shader.
While this works nicely, it has a couple of negative drawbacks - increased bandwidth from the use of gl_FragDepth; it also breaks depth-related optimizations etc. These issues can be addressed to some extent, results will depend on situation.
To compute the exact per-pixel value of logarithmic depth one has to interpolate the depth and then compute the logarithm in the fragment shader. While the logarithm seems to be a reasonably fast instruction on the GPU, we can get rid of it by using a trick.
The problem of depth interpolation appears mainly on close objects for specific reason - geometry of the objects is usually sufficiently tesselated only starting from a certain distance. Up close the triangles take a larger space on the screen, with interpolated values straying from the exact ones much more.
If we could linearize the logarithmic curve for the region close to the camera, we can simply output the interpolant directly without any code in the fragment shader.
Turns out that the C parameter in the equation can be used for that linearization. The following graph compares the N/F logarithmic function with the one with tunable C. N/F provides higher precision close to the near plane. However, that’s not where we actually need a better precision - our eye can’t even focus properly at those distances, there’s no need to have sub-micrometer resolutions there.
 By adjusting the C coefficient we can change the width of the flat part (which corresponds to a linear part of the depth mapping function), tuning it to the width we need for our scene and tesselation parameters. For C=1 the linear part is not deep enough to hide the zooming errors, but C=0.01 it’s about 10 meters, which is enough for FPS style views.
By adjusting the C coefficient we can change the width of the flat part (which corresponds to a linear part of the depth mapping function), tuning it to the width we need for our scene and tesselation parameters. For C=1 the linear part is not deep enough to hide the zooming errors, but C=0.01 it’s about 10 meters, which is enough for FPS style views.
To use this you have to add a new output attribute to the vertex shader:
out float logz;
and change the post-projection code to the following:
const float FC = 1.0/log(far*C + 1);
//logz = gl_Position.w*C + 1; //version with fragment code
logz = log(gl_Position.w*C + 1)*FC;
gl_Position.z = (2*logz - 1)*gl_Position.w;
Fragment shader will then contain the matching input declaration and an assignment to gl_FragDepth:
in float logz;
void main() {
//gl_FragDepth = log(logz)*CF;
gl_FragDepth = logz;
...
}
While it doesn't seem to be boosting the performance in any significant way in comparison to the commented out version, it's interesting in that if we had a possibility to turn on the perspective interpolation for z (like with all other interpolants), we would be able to use it directly without needing to write fragment depth values. Then again, seeing that log instruction is very fast, it could be used in the depth hardware to compute values for depth comparison directly. Anyway, both would likely require a change at the hardware level.
Conservative depth
Writing to gl_FragDepth disables early-z optimizations, which can be a problem in certain situations.
Logarithmic functions are monotonous, so we could use ARB_conservative_depth
extension to provide a hint to the driver that depth values from the fragment shader always lie below (or above) the interpolated value. This allows to skip shader evaluation if the fragments would be discarded.
To use conservative depth you have to redeclare gl_FragDepth in the fragment shader:
#extension GL_ARB_conservative_depth : enable
layout(depth_less) out float gl_FragDepth;
At first one could think that the hint to provide would be depth_greater, since a secant on the logarithmic curve always lies below it. But, surprisingly, the proper hint is depth_less. It's because while the value of z is being interpolated linearly in the rasterizer, the interpolant which we use to set gl_FragDepth is interpolated perspectively by interpolating p/w and 1/w linearly and getting its correct value by dividing the two. That means it's a comparison between:
((1-t)*log(A+1) + t*log(B+1));
((1-t)*log(A+1)/A + t*log(B+1)/B)/((1-t)/A + t/B)
It turns out that the perspectively interpolated values go below the linearly intepolated ones.
With depth compare GL_LESS that means the values written to gl_FragDepth can be only closer to the camera. Unfortunately that's of no use for early-z rejects.
A bit of consolation may be that in Outerra we didn't measure any speedup even with an inverted hint, even though it clearly showed on the geometry bugs.
A performance comparison in Outerra. Since the terrain and grass are tesselated adaptively, they don't need writing depth in the fragment shader. In case of the "Logarithmic FS" column of the following tables, only the objects are using fragment shader that writes depth. The decrease in FPS then largely depends on the amount of screen (+overdraw) that's covered by the objects.
A scene with a large area of the screen writing fragment depth. No stencil operations used. Even though the depth buffer format is DEPTH32F_S8, if stencil is not being used it has the same performance on Nvidia as the DEPTH32F format.
Table shows frames per second.
Common depth buffer setups used in 3D graphics hardware to this day are woefully inadequate for the task. One can easily get artifacts known as z-fighting even with relatively limited scene depth range. Utilization of the available depth buffer values is quite horrible: half of the resolution is essentially wasted just in the distance from the near plane to twice that (short) distance. This leads to the need to move the near plane as far as possible, which is not very desirable in itself, and it’s still not enough as soon as you need to cover just a slightly extended detail range. It’s of course completely unusable for large scale rendering, with developers having to use various tricks that bring their own bag of complications.
This article talks about the ways to set up the depth buffer so that it's able to handle blades of grass in front of your eyes while also rendering objects hundreds of kilometers in distance. It's mostly biased towards OpenGL, but most of it applies to DirectX as well.
 |
| A typical scene in planetary engine Outerra: from blades of grass to several tens of kilometers distant mountains |
How the standard depth buffer works
Let’s go first into some details about the depth processing that aren’t immediately obvious, which nevertheless play a significant role in understanding the properties of depth buffering.
A common perspective depth buffer setup relies on the use of a standard projection matrix that involves setting the near and far clipping plane distances. While you can set the projection matrix in any way you want, a perspective-correct depth buffering will work only as long as the matrix satisfies certain conditions.
With the standard perspective OpenGL projection matrix, the value of w and z output from the vertex shader is usually computed as:
wp = -z
zp = z*(n+f)/(n-f) + 2fn/(n-f)
That means w ends up holding the positive depth from the camera plane, while z can be generally expressed as a linear equation:
zp = -az + b
or
zp = awp + b
Values from the vertex shader are then converted into the normalized device coordinates by dividing by w, and z thus becomes:
zndc = a + b/wp = a - b/z
After that it gets clipped to -1 .. 1 range.
DirectX uses 0..1 range for z, but the principle is the same.
Specification says that with perspective interpolation all vertex shader outputs are interpolated in perspective (by interpolating p/w and 1/w linearly and then dividing the two to get perspective-correct values), except for the value of z which will be interpolated linearly. Why is that?
It’s because the rendering API expects that you are using a projection matrix that has a 1/z term in it (the above mentioned a - b/z), and thus to interpolate it in a perspective-correct way the hardware has to (and will only) use a linear interpolation.
Now the problem is that this value is also used for the depth comparison. At the first look it may seem to be a fairly nice function to be used for depth: providing a finer resolution for the near objects, getting reduced with the distance where it’s needed less as the objects get smaller in perspective.
However, in reality the profile is horribly unsuitable because it wastes way too much of the available range for the close values. Half of the available range is packed into tiny distance from the near plane to twice the near plane distance.
If there was a possibility to turn on the perspective interpolation on the depth component (as it’s already done for other interpolants unless the noperspective qualifier is used), then we would have several good ways to radically enhance the depth buffer precision without interpolation artifacts. Alas, the hardware doesn’t seem to count with that possibility anymore, as the W-buffers has been gradually phased out.
Let’s take a look on what can be done about it using the available resources. First, what would be the ideal profile.
Optimal depth resolution profile
To avoid z-fighting artifacts, depth buffer should provide resolution that is proportional to the size of geometry needed to render a constant screen size image at different distances from the camera, across the whole depth range. Projected screen size is proportional to the reciprocal of geometry depth, 1/z. In other words, we are looking for a function whose derivative is proportional to 1/z. That function happens to be the logarithm.
To see how an ideal utilization of depth buffer values compares to the common setup, see the following graph with computed precision of the common pipeline with 32bit floats, compared to logarithmic depth buffers at 24 and 32 bits.
While the logarithmic distribution handles the 9 decades of depth detail range easily, a common depth buffer setup strides into the unusable region after its brief 4 decades. Four decades is roughly the range we can get with the normal depth buffer setup, after that the precision gets into the unusable region and the depth buffer can't resolve the depth values properly anymore. With the logarithmic buffer we have a plenty of reserve, in fact we could handle the scene with a 16 bit logarithmic depth buffer.
Note that the axes in the graph are using logarithmic scales, so anything rising faster than 10dB is actually degenerating very quickly.
Speaking of an ideal utilization, it’s desirable to add that there’s also a lower bound on the required depth buffer resolution that reflects the physiognomy of our eyes - we can’t focus on objects very close to our eyes, so there’s no need to have a micrometer resolutions for miniscule objects in front of us. This can be used to enhance the resolution elsewhere, as we’ll see later.
Floating-point depth buffers
If the values used for depth comparison were the depth values themselves, floating point values would be good for the depth buffering technique: closer to the viewer you get values near zero, for which floating point encoding provides higher precision by keeping the number of bits in mantissa constant and adjusting the exponent. The farther you go less depth resolution you need, since the screen size of distant objects goes down by ≈1/z.
Unfortunately, the value used for depth comparison is the 1/z function itself which has the unfortunate property of eating all the resolution on breakfast and then starving till evening.
The use of floating-point values in depth buffer doesn’t bring much if used directly: there’s an increased dynamic range close to zero, but since the depth buffer already uses most of the value range in this region, it’s not useful at all.
There’s a trick that can do something about it: swapping the near and far values will make use of the increased range of floating point for the distant part, instead of the near one. This is actually very effective: the increasing resolution of floating point number close to zero neatly compensates the dwindling resolution of 1/z function.
Here’s the graph showing the resolution of reversed floating point buffer in DirectX:
Reversed 32bit floating point depth buffer brings slightly better resolution than a 24bit logarithmic buffer (a 32bit logarithmic depth buffer is roughly 20X finer), consistent across the whole 9 decades. That’s pretty great. One downside is that in comparison to a 24 bit integer buffer it consumes 8 more bits that could be otherwise used for stencil. Before, on older hardware, the use of stencil consumed twice as much memory for the framebuffer, since the next available format was padded to 32bits, with higher bandwidth required as well. However, nowadays it's not a problem - stencil is kept separate and depth buffer is optimized/packed, and the only thing that remained is a bit misleading OpenGL enum.
You will also notice I mentioned DirectX explicitly. If you try the trick on OpenGL you will see zero improvement.
DirectX vs. OpenGL
As much as I am a fan of OpenGL and prefer it over DirectX, there are things in OpenGL that make me want to climb walls holding with fingernails.
Some time back someone decided that OpenGL normalized device coordinates should be in range -1 .. 1 on all 3 axes, including the z coordinate. Normally, one would place the camera into the center, projecting towards +z or -z. Z axis projects to the screen center, so it’s only logical that x and y would be symmetric, but Z?
For the screen depth axis it’s more natural to assume normalized coordinates in 0..1 range, from the camera (or the near plane) to the far plane. Especially when the depth values written into the depth buffer are also in range 0..1.
However, someone dreamed of a symmetric world and decided it should be more important to prefer the symmetry over the reason, and to have z in the -1 .. 1 range as well. Of course, then it needs to be reprojected into the depth buffer values by performing additional computation: 0.5*zc + 0.5
How this connects with the depth buffer precision issue? First, reversing the depth range does essentially nothing, because it just swaps the mapping of the near and far plane between -1 and 1, with the extra precision around the zero mapped to 2*near distance in both cases.
This can be helped by using a projection that maps the far plane to 0. Normally the 3rd row of the OpenGL projection matrix is
mapping the near plane to -1 and the far plane to 1. Changing it to
will map the far plane to 0 instead. This is essentially the reversed-depth DirectX projection matrix with an inverted sign, so that the depth function doesn't change (but it can be easily switched to 1..0 range).
Clipping still applies at 1.0, so one would have to use a custom clipping plane to clip at 0. But it can be also ignored if the situation allows it. For example, in Outerra there’s actually no need to clip geometry behind the far plane, as it’s usually set as far as possible anyway.
But using this alternative projection alone does not resolve the problem, the resolution is still miserable. The second part of the problem is the additive term in the remapping (0.5zc + 0.5). That 0.5 bias locks the floating point exponent and pretty much destroys any and all additional precision that the encoding of floating point values brings close to zero, since now there are just 24 bits of mantissa to handle the unfortunate 1/z shape. Hello, symmetry!
Fortunately, at least on Nvidia there’s a way to eliminate the bias by (indirectly) setting the mapping function via the glDepthRangedNV call with -1, 1 arguments, which effectively sets the DirectX-style mapping. Here’s the final resolution graph of a floating point depth buffer without the bias, with the far plane mapped to 0 in OpenGL. The resolution was actually measured on the 460 GTX GPU:
Update: glDepthRangedNV is exposed in AMD Catalyst 13.11 betav9.2 drivers
Also note that even though OpenGL 4.2+ specification removed the note saying that the core function glDepthRange arguments will be clamped to 0..1 range for floating-point depth buffers, implementations are apparently still allowed to clamp the values on use, effectively making the spec change somewhat useless. As of now the values are being clamped even on Nvidia, so we need to use glDepthRangedNV extension.
Logarithmic Depth Buffers
There are two issues with the above described bias-less floating point OpenGL depth buffer - the lack of universal support, and the increased memory and bandwidth requirements in case a stencil buffer is needed.
We can actually use the above mentioned ideal logarithmic distribution on all current hardware. First described on the Outerra blog - see the logarithmic depth buffer article. Thatcher Ulrich later came up with a slightly different version here.
Logarithmic depth buffer technique works by outputting the desired logarithmic value from the vertex shader, premultiplied by the value of w, to get rid of later implicit perspective division.
It’s quite easy to implement, you just need to add the following code in the vertex shader after your normal projection matrix multiply:
gl_Position.z = 2.0*log(gl_Position.w*C + 1)/log(far*C + 1) - 1;
gl_Position.z *= gl_Position.w;
or
gl_Position.z = 2.0*log(gl_Position.w/near)/log(far/near) - 1;
gl_Position.z *= gl_Position.w;
The latter is Ulrich’s variant (here referred to as “N-F”) that has a nice property of having a constant relative precision over the whole near-far range, but as we’ll see later, nice (or symmetric) isn’t always the best option.
Obviously, the constant part (2.0/log(far*C+1) or 2.0/log(far/near), respectively) can be optimized out into a constant or uniform variable.
Notice that the “C” variant doesn’t use a near plane distance, it has it set at 0.
This algorithm works well, providing excellent precision across the whole range with a huge reserve. But it also suffers on issues with long polygons close to the camera.
The problem is that the vertex shader computed value is correct only at the vertices, but the interpolated values at pixels can stray from the expected value because of two factors: non-linearity of the logarithmic function between two depth values, and the implicit linear (and not perspective) interpolation of the depth value in the rasterizer. To fix it, one has to output the correct value by writing to gl_FragDepth in the fragment shader.
While this works nicely, it has a couple of negative drawbacks - increased bandwidth from the use of gl_FragDepth; it also breaks depth-related optimizations etc. These issues can be addressed to some extent, results will depend on situation.
Getting rid of the fragment shader computation
To compute the exact per-pixel value of logarithmic depth one has to interpolate the depth and then compute the logarithm in the fragment shader. While the logarithm seems to be a reasonably fast instruction on the GPU, we can get rid of it by using a trick.
The problem of depth interpolation appears mainly on close objects for specific reason - geometry of the objects is usually sufficiently tesselated only starting from a certain distance. Up close the triangles take a larger space on the screen, with interpolated values straying from the exact ones much more.
If we could linearize the logarithmic curve for the region close to the camera, we can simply output the interpolant directly without any code in the fragment shader.
Turns out that the C parameter in the equation can be used for that linearization. The following graph compares the N/F logarithmic function with the one with tunable C. N/F provides higher precision close to the near plane. However, that’s not where we actually need a better precision - our eye can’t even focus properly at those distances, there’s no need to have sub-micrometer resolutions there.
 By adjusting the C coefficient we can change the width of the flat part (which corresponds to a linear part of the depth mapping function), tuning it to the width we need for our scene and tesselation parameters. For C=1 the linear part is not deep enough to hide the zooming errors, but C=0.01 it’s about 10 meters, which is enough for FPS style views.
By adjusting the C coefficient we can change the width of the flat part (which corresponds to a linear part of the depth mapping function), tuning it to the width we need for our scene and tesselation parameters. For C=1 the linear part is not deep enough to hide the zooming errors, but C=0.01 it’s about 10 meters, which is enough for FPS style views.To use this you have to add a new output attribute to the vertex shader:
out float logz;
and change the post-projection code to the following:
const float FC = 1.0/log(far*C + 1);
//logz = gl_Position.w*C + 1; //version with fragment code
logz = log(gl_Position.w*C + 1)*FC;
gl_Position.z = (2*logz - 1)*gl_Position.w;
Fragment shader will then contain the matching input declaration and an assignment to gl_FragDepth:
in float logz;
void main() {
//gl_FragDepth = log(logz)*CF;
gl_FragDepth = logz;
...
}
While it doesn't seem to be boosting the performance in any significant way in comparison to the commented out version, it's interesting in that if we had a possibility to turn on the perspective interpolation for z (like with all other interpolants), we would be able to use it directly without needing to write fragment depth values. Then again, seeing that log instruction is very fast, it could be used in the depth hardware to compute values for depth comparison directly. Anyway, both would likely require a change at the hardware level.
Conservative depth
Writing to gl_FragDepth disables early-z optimizations, which can be a problem in certain situations.
Logarithmic functions are monotonous, so we could use ARB_conservative_depth
extension to provide a hint to the driver that depth values from the fragment shader always lie below (or above) the interpolated value. This allows to skip shader evaluation if the fragments would be discarded.
To use conservative depth you have to redeclare gl_FragDepth in the fragment shader:
#extension GL_ARB_conservative_depth : enable
layout(depth_less) out float gl_FragDepth;
At first one could think that the hint to provide would be depth_greater, since a secant on the logarithmic curve always lies below it. But, surprisingly, the proper hint is depth_less. It's because while the value of z is being interpolated linearly in the rasterizer, the interpolant which we use to set gl_FragDepth is interpolated perspectively by interpolating p/w and 1/w linearly and getting its correct value by dividing the two. That means it's a comparison between:
((1-t)*log(A+1) + t*log(B+1));
((1-t)*log(A+1)/A + t*log(B+1)/B)/((1-t)/A + t/B)
It turns out that the perspectively interpolated values go below the linearly intepolated ones.
With depth compare GL_LESS that means the values written to gl_FragDepth can be only closer to the camera. Unfortunately that's of no use for early-z rejects.
A bit of consolation may be that in Outerra we didn't measure any speedup even with an inverted hint, even though it clearly showed on the geometry bugs.
Comparison
A performance comparison in Outerra. Since the terrain and grass are tesselated adaptively, they don't need writing depth in the fragment shader. In case of the "Logarithmic FS" column of the following tables, only the objects are using fragment shader that writes depth. The decrease in FPS then largely depends on the amount of screen (+overdraw) that's covered by the objects.
A scene with a large area of the screen writing fragment depth. No stencil operations used. Even though the depth buffer format is DEPTH32F_S8, if stencil is not being used it has the same performance on Nvidia as the DEPTH32F format.
Table shows frames per second.
|
The same scene but objects taking a smaller part of the screen, with less bandwidth needed for fragment depth writes. No stencil operations used.
Table shows frames per second.
|  |
A simple scene with water rendering using stencil. Because of the increased bandwidth needed for the depth and stencil (32b depth + 8b stencil), its performance goes down a bit in this Outerra scene. In other programs/cases that are fill-rate bound the difference can be higher.
Table shows frames per second.
|
Conclusion
There are several ways to significantly enhance the range and precision of depth buffers, unfortunately all of them rely on driver and hardware support. For OpenGL the absolute minimum would be the ability to get rid of the bias that OpenGL pipeline applies when remapping from normalized depth coordinates to depth buffer values; right now it's only possible on Nvidia. It's highly likely that other vendors will be able to support it since the same mode is used by DirectX.
The best option would be to implement HW support for optimal depth buffer utilization. This would allow to reduce the bandwidth needed for depth and stencil usage, since even 16 bit logarithmic buffers are able to handle planetary scale with perfect precision where one needs it. With a 24bit logarithmic buffer one can handle cosmic scales.The next best option would be the ability to enable perspective interpolation on the z component, allowing to use linear and logarithmic depths without a loss of performance.
In Outerra we are currently using the logarithmic depth buffer with a couple of optimizations. Neither conservative depth nor the linearization seem to bring any significant performance improvements for us, but the dynamic control of fragment depth writes for object rendering can reclaim it back in most cases, as only the objects that are not tesselated enough require it. From this point of view it would be interesting to use dynamic tesselation for polygons that cross certain depth range threshold, but this needs to be tested yet.



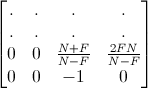





19 comments:
Wow, what a post! :)
Not so easy to understand but really really interesting.
P.S.: are those models coming with some new release? ;)
Yes, some of those probably will come, once we get the final permission to use them in Outerra.
Enjoyable read; very nicely explained.
The tables near the end could do with some units. I'm guessing the numbers are ms to render the image(?), since when you say performance goes down in the last one, the numbers get larger. But the only reference to what you're measuring is a "FPS" note in the intro paragraph of that section.
Thanks, I forgot to specify the units, added now - those are frames per second. In the last table performance goes down for the floating-point buffer (the first column).
Maybe be this article can be usefull: http://www.humus.name/index.php?page=Articles&ID=4 - about Just Cause 2 render (were not so big open spaces as Outerra but anyway about 30km range).
Any thoughts on reconstructing view space position from a D24S8 depth buffer storing logarithmic depth? I'm trying to use it in a deferred renderer for DX9 and get great depth precision... however, I didn't yet manage to get reconstruction working.
For encoding I use:
z = log(C * z + 1) / log(C * farClip + 1) * w;
When reading back from the depth buffer I've tried:
z = (pow(C * farClip + 1, depth) - 1) / C;
.. and then pass (x,y,z,1) through the inverse projection matrix to get view space position.
The inverse is ok, either:
z = (exp(d*log(C*far+1)) - 1)/C
or
z = (pow(C*far+1,d)-1)/C
z is the viewspace depth already, screenspace x and y need to be multiplied by z first and then by the projection inverse (but just x and y, since z is right already)
Why you are using gl_Position.w
when overriding gl_Position.z?
gl_Position.z = 2.0*log(gl_Position.w*C + 1)/log(far*C + 1) - 1;
i thought it should be
gl_Position.z = 2.0*log(gl_Position.z*C + 1)/log(far*C + 1) - 1;
Correct me if i`m wrong, please
When you use a normal projection matrix in OpenGL, gl_Position.w comes out as a positive depth from the camera, whereas gl_Position.z contains something expressible as a*z+b, what after perspective division by w falls into -1..1 range.
Since the logarithmic equation needs the depth from the camera, I'm using w there, otherwise I'd have to use a modified projection matrix where z comes out as the depth.
Being able to use an unchanged projection matrix makes it simpler to switch to the reverse floating point depth mode.
Thanks for detailed explanation!
So for now, the best solution for NVonly users would be:
0. use FP32 or D24\D32 depth buffer?
1. call glDepthRangedNV with -1,+1
2a. override z in VS as
gl_Position.z = 2.0*log(gl_Position.w*C + 1)/log(far*C + 1) - 1;
or
2b. draw with projection matrix you
've specified in 'DirectX vs. OpenGL' part of your article; invert depth test to GL_GREATER\GL_GEQUAL;
override z in VS as
gl_Position.z = 2.0*log(gl_Position.z*C + 1)/log(far*C + 1) - 1;
3. gl_Position.z *= gl_Position.w;
Just don't understand which combination would be best possible on NV hardware (stencil is not used at all)...
Would you give an advice for this case, please?
Thanks!
If you are NV-only and no stencil, the best thing would be to use the reverse floating point depth buffer. You are safe from depth artifacts that way, and performance-wise it's almost the same as with the logarithmic 24b depth.
To use the reverse FP depth buffer in OpenGL, you need to:
- use FP32 depth buffer format
- call glDepthRangedNV(-1,+1)
- use the DX-like matrix from 'DirectX vs. OpenGL' part of the article, together with GL_LESS depth func (the matrix can be also modified to invert the mapping to use GL_GREATER)
No modification to gl_Position is done here in this case, you just use the matrix in normal way.
Thanks! I`ll try it out
How can I restore the worldspace position of a pixel from screenspace position and depth ?
This is what I use for a standard depth buffer:
vec3 getPosition(in float depth, in vec2 uv){
vec4 pos = vec4(uv, depth, 1.0) * 2.0 - 1.0;
pos = m_ViewProjectionMatrixInverse * pos;
return pos.xyz / pos.w;
}
My logarithmic depth is calculated like this:
logz = log(gl_Position.w * C + 1.0) * FC;
gl_Position.z = (2.0 * logz - 1.0) * gl_Position.w;
With depth value from the depth buffer in range 0..1, the camera depth is:
(exp(depth/FC)-1.0)/C
Since you are using logarithmic depth, you can use projection matrix that produces camera depth in z component (since it's not used in shaders anymore), in OpenGL by setting proj[2][2]=0 and proj[3][2]=-1
Make the inverse viewproj matrix from the viewproj matrix made from the view matrix and this updated projection matrix. Then you can simply use your existing routine to compute the worldspace position from uv and the camera depth computed above.
I believe it should be proj[2][2]=-1 and proj[3][2]=0, because they way you wrote z_p will always be calculates as -1. Either way it does not work...
You are right, I swapped them mistakenly.
But otherwise it should work, you probably have to debug it with some simple cases to see if it produces the right signs and values.
if you did this 10 years ago, I am eager to see what you're doing now
I am using the following log conversion in my vertex shader:
gl_Position.z = 2.0*log(gl_Position.w/near)/log(far/near) - 1;
gl_Position.z *= gl_Position.w;
if I read from the depth buffer how can can I convert the log depth back to the normal value? Is there another work around if I need the depth value in a fragment shader?
Electronics Components are the building blocks of modern technology, driving innovation and functionality.
Post a Comment