Written mainly for my own reference, but it's also possible that someone else finds it useful as well.
The problem: OpenGL specification/extension ARB_gpu_shader_fp64 that brings support for double precision operations on the GPU specifically states that double-precision versions of angle, trigonometry, and exponential functions are not supported. All we get are the basic add/mul operations and sqrt.
In rendering planetary-scaled geometry you'll often hit numerical precision issues, and it's a good idea to avoid using 64-bit floats altogether because they come at a price. Performance hit is usually even larger than it could be, as some vendors intentionally cripple the double precision operations, to make a greater gap between their consumer and professional GPU lines.
In some cases it's not worth going into the trouble of trying to solve both the performance and precision problems at once, for example in tools that process real world data or project maps. These usually need trigonometric functions when converting between different map projection types, and a higher precision than 32 bit floats can give.
Unless one can/want to use OpenCL interoperation, here are some tricks how to reduce some of the used equations to just the basic supported double-precision operations.
In our case we needed to implement the geographic and Mercator projections. For both we need atan (or better atan2) function, which we'll get through a polynomial approximation.
Article on Lol Engine blog colorfully talks about why it's not a good idea to use Taylor series for approximating functions over an interval, and compares it with Ramez/minimax method. What's nice is that the good folks also released a tool for computing the minimax approximations, called remez exchange toolbox. Using this tool we can get a good atan approximation with custom adjustable polynomial degree / maximum error.
Here's the source code for the atan2 approximation with error less than 5 ⋅ 10-9, computed using the lolremez tool. Angular error of 5 ⋅ 10-9 translates to ~ 3cm error on Earth surface, which is very good for our purposes.
Where φ is the latitude angle. Bad luck, neither ln nor tan functions are available with double arguments. Logarithm approximation doesn't give a good precision with reasonable polynomial degree, but it turns out we actually do not need to approximate neither ln nor tan function.
It follows that:
Given that, going from 3D coordinates, we can get the value of tan φ simply from the 3D coordinates (assuming ECEF coordinate system):
Meaning that the inner logarithm expression now consists solely of operations that are supported by the ARB_gpu_shader_fp64 extension.
Finally, we can get rid of the logarithm itself by utilizing the identity:
and using the single-precision logarithm function to compute a delta value from some reference angle computed on the CPU. Typically that means computing sqrt(k^2+1) + |k| for the screen coordinate center, and using the computed logarithm difference directly as the projected screen y coordinate.
Since the resulting value of a/b is very close to 1 in cases when we need extra double precision (zoomed in), we can even use the crudest ln approximation around 1: ln(x) ≅2*x/(2+x) with double arithmetic.
@cameni
The problem: OpenGL specification/extension ARB_gpu_shader_fp64 that brings support for double precision operations on the GPU specifically states that double-precision versions of angle, trigonometry, and exponential functions are not supported. All we get are the basic add/mul operations and sqrt.
In rendering planetary-scaled geometry you'll often hit numerical precision issues, and it's a good idea to avoid using 64-bit floats altogether because they come at a price. Performance hit is usually even larger than it could be, as some vendors intentionally cripple the double precision operations, to make a greater gap between their consumer and professional GPU lines.
In some cases it's not worth going into the trouble of trying to solve both the performance and precision problems at once, for example in tools that process real world data or project maps. These usually need trigonometric functions when converting between different map projection types, and a higher precision than 32 bit floats can give.
Unless one can/want to use OpenCL interoperation, here are some tricks how to reduce some of the used equations to just the basic supported double-precision operations.
fp64 atan2 approximation
In our case we needed to implement the geographic and Mercator projections. For both we need atan (or better atan2) function, which we'll get through a polynomial approximation.
Article on Lol Engine blog colorfully talks about why it's not a good idea to use Taylor series for approximating functions over an interval, and compares it with Ramez/minimax method. What's nice is that the good folks also released a tool for computing the minimax approximations, called remez exchange toolbox. Using this tool we can get a good atan approximation with custom adjustable polynomial degree / maximum error.
Here's the source code for the atan2 approximation with error less than 5 ⋅ 10-9, computed using the lolremez tool. Angular error of 5 ⋅ 10-9 translates to ~ 3cm error on Earth surface, which is very good for our purposes.
// atan2 approximation for doubles for GLSL
// using http://lolengine.net/wiki/doc/maths/remez
double atan2(double y, double x)
{
const double atan_tbl[] = {
-3.333333333333333333333333333303396520128e-1LF,
1.999999117496509842004185053319506031014e-1LF,
-1.428514132711481940637283859690014415584e-1LF,
1.110012236849539584126568416131750076191e-1LF,
-8.993611617787817334566922323958104463948e-2LF,
7.212338962134411520637759523226823838487e-2LF,
-5.205055255952184339031830383744136009889e-2LF,
2.938542391751121307313459297120064977888e-2LF,
-1.079891788348568421355096111489189625479e-2LF,
1.858552116405489677124095112269935093498e-3LF
};
/* argument reduction:
arctan (-x) = -arctan(x);
arctan (1/x) = 1/2 * pi - arctan (x), when x > 0
*/
double ax = abs(x);
double ay = abs(y);
double t0 = max(ax, ay);
double t1 = min(ax, ay);
double a = 1 / t0;
a *= t1;
double s = a * a;
double p = atan_tbl[9];
p = fma( fma( fma( fma( fma( fma( fma( fma( fma( fma(p, s,
atan_tbl[8]), s,
atan_tbl[7]), s,
atan_tbl[6]), s,
atan_tbl[5]), s,
atan_tbl[4]), s,
atan_tbl[3]), s,
atan_tbl[2]), s,
atan_tbl[1]), s,
atan_tbl[0]), s*a, a);
double r = ay > ax ? (1.57079632679489661923LF - p) : p;
r = x < 0 ? 3.14159265358979323846LF - r : r;
r = y < 0 ? -r : r;
return r;
}
Mercator projection
While the geographic projection can do with the above atan2 function to compute the longitude and latitude, Mercator uses a different mapping for the y-axis, to preserve the shapes:Where φ is the latitude angle. Bad luck, neither ln nor tan functions are available with double arguments. Logarithm approximation doesn't give a good precision with reasonable polynomial degree, but it turns out we actually do not need to approximate neither ln nor tan function.
It follows that:
Given that, going from 3D coordinates, we can get the value of tan φ simply from the 3D coordinates (assuming ECEF coordinate system):
Meaning that the inner logarithm expression now consists solely of operations that are supported by the ARB_gpu_shader_fp64 extension.
Finally, we can get rid of the logarithm itself by utilizing the identity:
and using the single-precision logarithm function to compute a delta value from some reference angle computed on the CPU. Typically that means computing sqrt(k^2+1) + |k| for the screen coordinate center, and using the computed logarithm difference directly as the projected screen y coordinate.
Since the resulting value of a/b is very close to 1 in cases when we need extra double precision (zoomed in), we can even use the crudest ln approximation around 1: ln(x) ≅2*x/(2+x) with double arithmetic.
@cameni


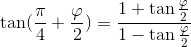


No comments:
Post a Comment